Câu hỏi
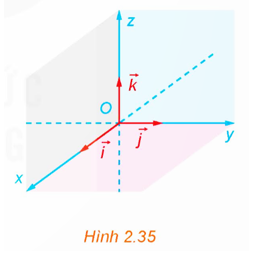
05/12/2024 4Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME có ba đỉnh A, B, C lần lượt thuộc các tia Ox, Oy, Oz (H.2.37).
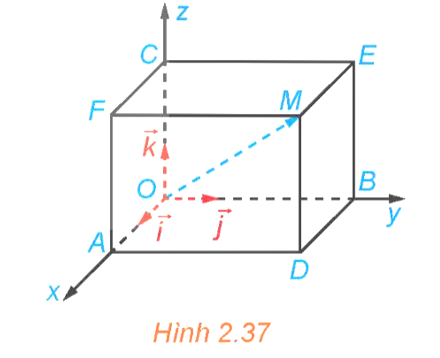
a) Hai vectơ và có bằng nhau không?
b) Giải thích vì sao có thể viết với x, y, z là các số thực.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Do OADB.CFME là hình hộp chữ nhật nên theo quy tắc hình hộp ta có:
b) Vì là vectơ đơn vị trên trục Ox nên ta có với x là số thực.
Vì là vectơ đơn vị trên trục Oy nên ta có với y là số thực.
Vì là vectơ đơn vị trên trục Oz nên ta có với z là số thực.
Vì vậy với x, y, z là các số thực.