Câu hỏi
22/11/2024 12Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (H.1.14). Tính cạnh của các hình vuông bị cắt sao cho thể tích của chiếc hộp là lớn nhất.

Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Gọi x (cm) là độ dài cạnh của các hình vuông nhỏ được cắt ở bốn góc của tấm bìa.
Điều kiện 0 < x < 30.
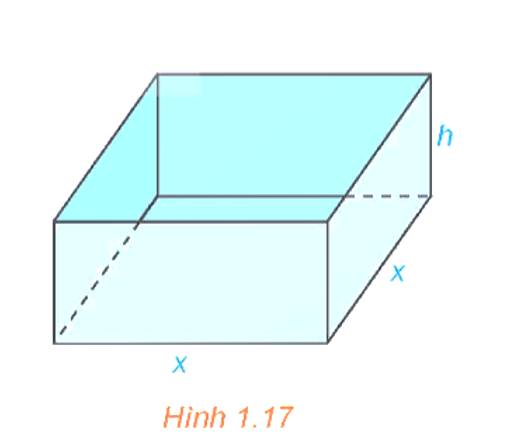
Khi cắt bỏ bốn hình vuông nhỏ có cạnh x (cm) ở bốn góc và gập lên thì ta được một chiếc hộp chữ nhật không có nắp, có đáy là hình vuông với độ dài cạnh bằng (60 – 2x) (cm) và chiều cao bằng x (cm).
Thể tích của chiếc hộp này là: V(x) = (60 – 2x)2.x = 4x3 – 240x2 + 3600x (cm3).
Ta có V'(x) = 12x2 – 480x + 3600;
V'(x) = 0 Û 12x2 – 480x + 3600 = 0 Û x = 10 (thỏa mãn) hoặc x = 30 (loại).
Lập bảng biến thiên

Như vậy để thể tích của chiếc hộp lớn nhất thì độ dài cạnh của các hình vuông nhỏ phải cắt là 10 cm.

![Cho hàm số y = f(x) = x^2 – 2x với x ∈ [0; 3], có đồ thị như hình 1.15. (ảnh 1)](https://vuatracnghiem.vn/wp-content/uploads/2024/11/Cho-ham-so-y-fx-x2-–-2x.png)
![Xét hàm số y = f(x) = x3 – 2x2 + 1 trên đoạn [−1; 2] với đồ thị như hình 1.16 (ảnh 1)](https://vuatracnghiem.vn/wp-content/uploads/2024/11/Xet-ham-so-y-fx-x3-–-2x2.png)