Câu hỏi
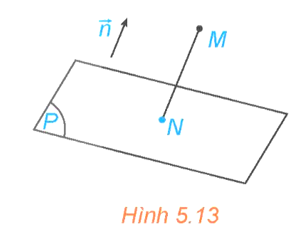
19/12/2024 2Trong không gian Oxyz, cho mặt phẳng (α). Gọi là một vectơ pháp tuyến của (α) và M0(x0; y0; z0) là một điểm thuộc (α).
a) Một điểm M(x; y; z) thuộc (α) khi và chỉ khi hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_0}M} \) có mối quan hệ gì?
b) Điểm M(x; y; z) thuộc (α) khi và chỉ khi tọa độ của nó thỏa mãn hệ thức nào?
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Ta có \(\overrightarrow {{M_0}M} = \left( {x – {x_0};y – {y_0};z – {z_0}} \right)\)
\(\overrightarrow n = \left( {A;B;C} \right)\) là một vectơ pháp tuyến của (α) nên \(\overrightarrow n \bot \overrightarrow {{M_0}M} \).
Suy ra \(\overrightarrow n .\overrightarrow {{M_0}M} = \overrightarrow 0 \) Û A(x – x0) + B(y – y0) + C(z – z0) = 0.
Do đó một điểm M(x; y; z) thuộc (α) khi và chỉ khi hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_0}M} \) vuông góc với nhau.
b) Từ câu a, ta có A(x – x0) + B(y – y0) + C(z – z0) = 0
Û Ax + By + Cz = Ax0 + By0 + Cz0
Û Ax + By + Cz = D (trong đó D = Ax0 + By0 + Cz0).
Do đó điểm M(x; y; z) thuộc (α) khi và chỉ khi tọa độ của nó thỏa mãn hệ thức Ax + By + Cz = D trong đó \(\overrightarrow n = \left( {A;B;C} \right)\) và D = Ax0 + By0 + Cz0.