Chiều cao của 20 cây xoan giống (đơn vị là cm) được cho như sau:

a) Tính độ lệch chuẩn của s_g của mẫu số liệu.

b) Hoàn thiện bảng số liệu ghép nhóm sau và tính độ lệch chuẩn s_n của mẫu số liệu ghép nhóm này:

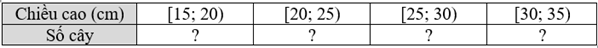
c) Nên dùng giá trị s_g hay s_n để đo mức độ phân tán về chiều cao của 20 cây giống xoan này?

Lời giải của Vua Trắc Nghiệm

a) Tổng chiều cao 20 cây xoan giống đó là:

15 + 19 + 24 + 31 + 27 + 23 + 18 + 19 + 25 + 29 + 23 + 33 + 34 + 27 + 31 + 24 + 27

+ 21 + 29 + 30 = 509.

Chiều cao trung bình của 20 cây xoan giống là: \(\frac{{509}}{{20}}\) = 25,45.

Ta có: Tổng bình phương của 20 giá trị số liệu trong bảng là:

15² + 19² + 24² + 31² + 27² + 23² + 18² + 19² + 25² + 29² + 23² + 33² + 34² + 27² + 31²

+ 24² + 27² + 21² + 29² + 30² = 13 483.

Lúc này, độ lệch chuẩn của mẫu số liệu gốc là:

S_g = \(\sqrt {\frac{1}{{20}}.13483 – 25,{{45}^2}} \) ≈ 5,14.

b) Ta có bảng số liệu ghép nhóm:

Chọn giá trị đại diện cho mỗi nhóm số liệu, ta có bảng sau:

Chiều cao trung bình của mỗi cây trong mẫu dữ liệu ghép nhóm là

\(\overline x \) = \(\frac{{4.17,5 + 5.22,5 + 6.27,5 + 5.32,5}}{{20}}\) = 25,5.

Độ lệch chuẩn là:

s = \(\sqrt {\frac{1}{{20}}\left( {4.17,{5^2} + 5.22,{5^2} + 6.27,{5^2} + 5.32,{5^2}} \right) – 25,{5^2}} \) ≈ 5,34.

c) Từ số liệu tính được phần a, b ta nên dùng giá trị s_g để đo mức độ phân tán về chiều cao của 20 cây xoan giống.