Câu hỏi
26/11/2024 27Cho điểm A(3; 2) trên mặt phẳng tọa độ. Một đường thẳng đi qua A cắt trục hoành tại B, cắt trục tung tại C tạo thành một tam giác OBC nằm trong góc phần tư thứ nhấ, với O là gốc tọa độ.
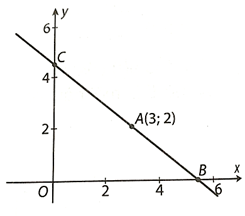
a) Biết hoành độ điểm B là x = t với t > 3. Tính diện tích tam giác OBC theo t. Kí hiệu diện tích này là S(t).
b) Khảo sát sự biến thiên của hàm số S(t).
c) Tìm vị trí điểm B để diện tích tam giác OBC là nhỏ nhất.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Ta có: B(t; 0).
Suy ra \(\overrightarrow {AB} \) = (t – 3; −2).
Phương trình đường thẳng AB là: \(\frac{{x – 3}}{{t – 3}} = \frac{{y – 2}}{{ – 2}}\) hay y = 2 − \(\frac{2}{{t – 3}}\left( {x – 3} \right)\).
Suy ra điểm C có tung độ yC = 2 + \(\frac{6}{{t – 3}}\).
Vậy C\(\left( {0;2 + \frac{6}{{t – 3}}} \right)\).
Ta có: OB = \(\sqrt {{{\left( {t – 0} \right)}^2} + {{\left( {0 – 0} \right)}^2}} \) = t
OC = \(\sqrt {{{\left( {0 – 0} \right)}^2} + {{\left( {2 + \frac{6}{{t – 3}} – 0} \right)}^2}} = \frac{{2t}}{{t – 3}}\).
Diện tích tam giác OBC là S(t) = \(\frac{1}{2}\).OB.OC = \(\frac{1}{2}\).t.\(\frac{{2t}}{{t – 3}}\) = \(\frac{{{t^2}}}{{t – 3}}\).
b) Khảo sát sự biến thiên của hàm số S(t) = \(\frac{{{t^2}}}{{t – 3}}\).
1. Tập xác định: D = (3; +∞).
2. Sự biến thiên
Giới hạn tại vô cực, giới hạn vô cực: \(\mathop {\lim }\limits_{t \to {3^ + }} S(t) = + \infty ;\mathop {\lim }\limits_{t \to + \infty } S(t) = + \infty \).
Ta có: S(t) = t + 3 +\(\frac{9}{{t – 3}}\).
S‘(t) = 1 − \(\frac{9}{{{{\left( {t – 3} \right)}^2}}}\)
S‘(t) = 0 ⇔ 1 − \(\frac{9}{{{{\left( {t – 3} \right)}^2}}}\) = 0 ⇔ t = 6 (do t > 3).
Ta có bảng biến thiên như sau:

Hàm số đạt cực tiểu tại t = 6 và yCT = 12.
c) Dựa vào bảng biến thiên ở phần b, ta thấy để diện tích tam giác OBC có diện tích nhỏ nhất thì B(6; 0).


![Gia tốc a(t) của một vật chuyển động, t tính theo giây, từ giây thứ nhất đến giây thứ 5 là một hàm liên tục có đồ thị như hình sau: a) Lập bảng biến thiên của hàm vận tốc y = v(t) của vật, với t ∈ [1; 5]. b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất? (ảnh 1)](https://vuatracnghiem.vn/wp-content/uploads/2024/11/Gia-toc-at-cua-mot-vat-chuyen-dong-t-tinh.png)
