Câu hỏi
06/12/2024 8Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1. Xét hệ tọa độ Oxyz gắn với hình lập phương như hình vẽ bên.
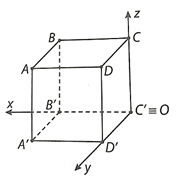
a) Tìm tọa độ các đỉnh của hình lập phương.
b) Tìm tọa độ trọng tâm G của tam giác B’CD’.
c) Chứng minh rằng ba điểm O, G, A thẳng hàng.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Ta có: C‘(0; 0; 0), D‘(0; 1; 0), B‘(1; 0; 0); C(0; 0; 1); D(0; 1; 1).
Ta có: \(\overrightarrow {CC’} = \overrightarrow {AA’} = \overrightarrow {BB’} = \overrightarrow {DD’} \) = (0; 0; −1).
Gọi B(x; y; z), ta có: \(\left\{ \begin{array}{l}1 – x = 0\\0 – y = 0\\0 – z = – 1\end{array} \right.\)⇔ \(\left\{ \begin{array}{l}x = 1\\y = 0\\z = 1\end{array} \right.\).
Do đó B(1; 0; 1).
Ta có: \(\overrightarrow {AB} = \overrightarrow {DC} \) ⇒ A(1; 1; 1).
\(\overrightarrow {CC’} = \overrightarrow {AA’} \)⇒ A‘ (1; 1; 0).
b) Gọi G(xG; yG; zG), ta có:
\(\left\{ \begin{array}{l}{x_G} = \frac{{1 + 0 + 0}}{3} = \frac{1}{3}\\{y_G} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\\{z_G} = \frac{{0 + 0 + 1}}{3} = \frac{1}{3}\end{array} \right.\).
Do đó G\(\left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\).
c) Ta có: \(\overrightarrow {OG} = \left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\), \(\overrightarrow {OA} = (1;1;1).\)
Có \(\overrightarrow {OG} = \frac{1}{3}\overrightarrow {OA} \) cho nên ba điểm O, G, A thẳng hàng.