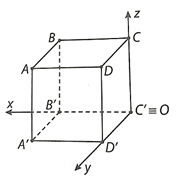
Cho tứ diện ABCD. Trọng tâm G của tứ diện là điểm duy nhất thỏa mãn đẳng thức \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Chứng minh rằng tọa độ của điểm G được cho bởi công thức:

x_G = \(\frac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4}\);

y_G = \(\frac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4}\);

z_G = \(\frac{{{z_A} + {z_B} + {z_C} + {z_D}}}{4}\).

Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a \) = (3; 0; 4), \(\overrightarrow b \) = (2; 7; 7) và \(\overrightarrow c \) = (2; 7; 2).

a) Tìm tọa độ của các vectơ \(\overrightarrow a – \overrightarrow b + \overrightarrow c \) và \(2\overrightarrow a + 3\overrightarrow b – 4\overrightarrow c \).

b) Tính các tích vô hướng \(\left( { – \overrightarrow a } \right).\overrightarrow b \) và \(\left( {3\overrightarrow a } \right)\).\(\overrightarrow c \).

c) Tính côsin của các góc \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) và \(\left( {\overrightarrow a ,\overrightarrow c } \right)\).

Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a \) = (m; 3; 6) và \(\overrightarrow b \) = (1; 2; 3). Xác định giá trị của m trong những trường hợp sau:

a) \(\overrightarrow a – 2\overrightarrow b \) = (3; −1; 0);

b) \(\overrightarrow a .\overrightarrow b \) = 10;

c) \(\left| {\overrightarrow a } \right|\) = 9.

Trong không gian Oxyz, cho tứ diện ABCD với A(1; 3; −3), B(2; 0; 5), C(6; 9; −5) và D(−1; −4; 3).

a) Tìm tọa độ trọng tâm I của tam giác ABC.

b) Tìm tọa độ của điểm G thuộc đoạn thẳng DI sao cho DG = 3IG.

Trong không gian Oxyz, cho tam giác ABC với A(3; 5; 2), B(0; 6; 2) và C(2; 3; 6). Hãy giải tam giác ABC.

Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1. Xét hệ tọa độ Oxyz gắn với hình lập phương như hình vẽ bên.

a) Tìm tọa độ các đỉnh của hình lập phương.

b) Tìm tọa độ trọng tâm G của tam giác B’CD’.

c) Chứng minh rằng ba điểm O, G, A thẳng hàng.

Trên sân thể dục thầy giáo dựng hai chiếc cột vuông góc với mặt sân, chiều cao của mỗi chiếc cột lần lượt là 3 m và 2 m. Xét hệ tọa độ Oxyz sao cho mặt phẳng (Oxy) trùng với mặt sân, trục Oz hướng thẳng đứng lên trời. Đơn vị trong hệ tọa độ Oxyz được lấy theo mét.

a) Biết rằng chân của hai cột đó có tọa độ lần lượt là (8; 5; 0) và (3; 2; 0), hãy tìm tọa độ điểm đầu của mỗi cột.

b) Thầy giáo dự định căng một sợi dây nối hai đầu của hai cột. Hỏi sợi dây cần có độ dài tối thiểu là khoảng bao nhiêu mét?

Hình bên mô tả hai bức tường gạch được xây vuông góc với nhau và cùng vuông góc với mặt đất. Một người thợ xây căng dây giữa hai bức tường. Đầu A của sợi dây nằm trên bức tường thứ nhất, cách bức tường thứ hai là 3 m và cách mặt đất là 1,2 m. Đầu B của sợi dây nằm trên bức tường thứ hai, cách bức tường thứ nhất là 1 m và cách mặt đất là 2 m.

a) Hãy lập một hệ trục tọa độ phù hợp và tìm tọa độ của hai đầu A, B trong hệ tọa độ đó.

b) Tính độ dài của sợi dây được căng.