Câu hỏi
17/12/2024 2Tính diện tích của các hình phẳng được tô màu dưới đây:
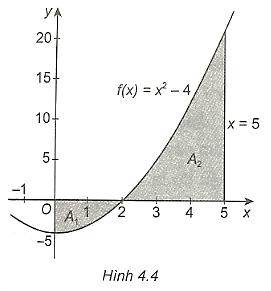
a)
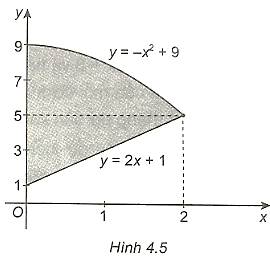
b)
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Hình phẳng được giới hạn bởi các đường và
Diện tích cần tính là:
S = \(\int\limits_0^5 {\left| {{x^2} – 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} – 4} \right|dx} + \int\limits_2^5 {\left| {{x^2} – 4} \right|dx} \)
= \(\int\limits_0^2 {\left( {4 – {x^2}} \right)dx} + \int\limits_2^5 {\left( {{x^2} – 4} \right)dx} \)
= \(\left. {\left( {4x – \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} – 4x} \right)} \right|_2^5\)
= 4.2 – \(\frac{8}{3}\) − 4.0 + \(\frac{0}{3}\) + \(\frac{{{5^3}}}{3}\) − 4.5 – \(\frac{8}{3}\) + 4.2 = \(\frac{{97}}{3}\).
b) Hình phẳng cần tìm được giới hạn bởi các đường và
Diện tích cần tính là:
S = \(\int\limits_0^2 {\left| { – {x^2} + 9 – \left( {2x + 1} \right)} \right|dx} \) = \(\int\limits_0^2 {\left| { – {x^2} – 2x + 8} \right|} dx\)
= \(\int\limits_0^2 {\left( { – {x^2} – 2x + 8} \right)dx} \)
= \(\left. {\left( {\frac{{ – {x^3}}}{3} – {x^2} + 8x} \right)} \right|_0^2\) = \(\frac{{28}}{3}\).