Câu hỏi
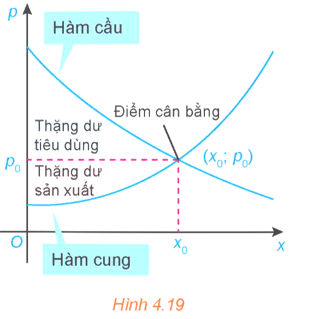
17/12/2024 3Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi x là đại diện cho phần trăm số gia đình trong một quốc gia và y là phần trăm tổng thu nhập, mô hình y = x sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz y = f(x), biểu thị phân phối thu nhập thực tế. Diện tích giữa hai mô hình này, với 0 ≤ x ≤ 100, biểu thị “sự bất bình đẳng về thu nhập” của một quốc gia. Năm 2005, đường con Lorenz của Hoa Kỳ có thể được mô hình hóa bởi hàm số
y = (0,00061x2 + 0,0218x + 1723)2, 0 ≤ x ≤ 100,
trong đó x được tính từ các gia đình nghèo nhất đến giàu có nhất (Theo R.Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009).
Tìm sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005 là:
\(S = \int\limits_0^{100} {\left| {{{\left( {0,00061{x^2} + 0,0218x + 1723} \right)}^2} – x} \right|dx} \)
\( = \int\limits_0^{100} {\left| {\left( {{{0,00061}^2}{x^4} + {{4,7524.10}^{ – 4}}{x^2} + {{1723}^2} + {{2,6596.10}^{ – 5}}{x^3} + 2,10206{x^2} + 75,1228x} \right) – x} \right|dx} \)
\( = \int\limits_0^{100} {\left| {\left( {{{0,00061}^2}{x^4} + {{2,6596.10}^{ – 5}}{x^3} + 2,10253524{x^2} + 74,1228x + {{1723}^2}} \right)} \right|dx} \)
\( = \int\limits_0^{100} {\left( {{{0,00061}^2}{x^4} + {{2,6596.10}^{ – 5}}{x^3} + 2,10253524{x^2} + 74,1228x + {{1723}^2}} \right)dx} \)
\[ = \left. {\left( {{{7,442.10}^{ – 8}}.{x^5} + {{6,649.10}^{ – 6}}.{x^4} + 0,70084508.{x^3} + 37,0614.{x^2} + {{1723}^2}.x} \right)} \right|_0^{100}\]
\[ = {7,442.10^{ – 8}}{.100^5} + {6,649.10^{ – 6}}{.100^4} + {0,70084508.100^3} + {37,0614.100^2} + {1723^2}.100\]
= 297945768,2.