Câu hỏi
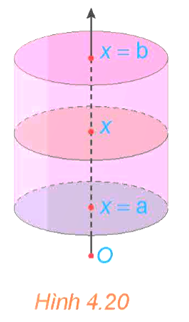
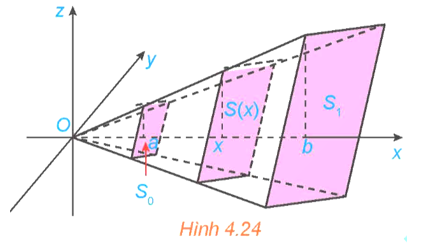
17/12/2024 1Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S0, S1 và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Chọn hệ trục tọa độ Oxyz như hình vẽ.
Gọi a và b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn của hình chóp. Khi đó chiều cao của hình chóp cụt là h = b – a.
Thiết diện của khối chóp cụt khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b) là một đa giác đều đồng dạng với đáy lớn của hình chóp cụt theo tỉ số đồng dạng là \(\frac{x}{b}\).
Khi đó \(\frac{{S\left( x \right)}}{{{S_1}}} = \frac{{{x^2}}}{{{b^2}}} \Rightarrow S\left( x \right) = \frac{{{x^2}}}{{{b^2}}}.{S_1}\).
Vì vậy thể tích khối chóp cụt đều là:
\(V = \int\limits_a^b {S\left( x \right)} dx = \int\limits_a^b {\frac{{{x^2}}}{{{b^2}}}{S_1}} dx = \left. {\frac{{{S_1}}}{{{b^2}}}.\frac{{{x^3}}}{3}} \right|_a^b\)\( = \frac{{{S_1}}}{{3{b^2}}}\left( {{b^3} – {a^3}} \right)\)
\( = \frac{{b – a}}{{3{b^2}}}.\left( {{S_1}{b^2} + {S_1}ab + {S_1}{a^2}} \right)\)\( = \frac{h}{3}.\left[ {{S_1} + {S_1}\frac{a}{b} + {S_1}{{\left( {\frac{a}{b}} \right)}^2}} \right]\).
Vì \(\frac{{{S_0}}}{{{S_1}}} = {\left( {\frac{a}{b}} \right)^2} \Rightarrow {S_0} = {S_1}.{\left( {\frac{a}{b}} \right)^2}\); \({S_0}{S_1} = S_1^2.{\left( {\frac{a}{b}} \right)^2}\)\( \Rightarrow \sqrt {{S_0}{S_1}} = {S_1}.\frac{a}{b}\).
Vì vậy \(V = \frac{h}{3}.\left[ {{S_1} + \sqrt {{S_1}.{S_0}} + {S_0}} \right]\).
Khối chóp đều được coi là khối chóp cụt đều khi S0 = 0.
Vì vậy thể tích khối chóp đều là: \(V = \frac{1}{3}.S.h\).