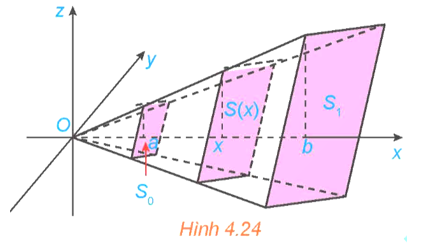
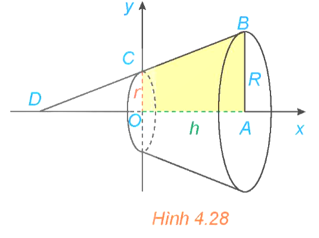
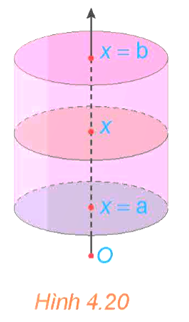
Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20).

a) Tính thể tích V của hình trụ.

b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b). Từ đó tính $\underset{a}{\overset{b}{\int }}S\left(x\right)dx$ và so sánh với V.

Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12).

a) Tính diện tích S của hình phẳng này.

b) Tính $\underset{-2}{\overset{1}{\int }}\left|f\left(x\right)\right|dx$ và so sánh với S.

Tính diện tích hình phẳng giới hạn bởi parabol y = x² – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15).

Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x² + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16).

a) Giả sử S₁ là diện tích hình phẳng giới hạn bởi parabol y = −x² + 4x, trục hoành và hai đường thẳng x = 1, x = 3; S₂ là diện tích hình phẳng giới hạn bởi đường thẳng y = x, trục hoành và hai đường thẳng x = 1, x = 3. Tính S₁, S₂ và từ đó suy ra S.

b) Tính $\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$ và so sánh với S.

Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y=\sqrt{x}$, y = x – 2 và hai đường thẳng x = 1, x = 4.

Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x₀; p₀) của đồ thị hàm cầu p = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p₀ và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p₀ và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R.Larson, Brief Calculus: An Applied Approach, 8^th edition, Cengage Learning, 2009).

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: p = −0,36x + 9 và hàm cung: p = 0,14x + 2, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S₀, S₁ và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Xét hình phẳng giới hạn bởi đồ thị hàm số $f\left(x\right)=\frac{1}{2}x$, trục hoành và hai đường thẳng x = 0, x = 4. Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).

a) Tính thể tích V của khối nón.

b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (0 ≤ x ≤ 4) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là S(x) = πf²(x). Tính $\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$ và so sánh với V.

a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r, quanh trục Ox (H.4.28).

b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.

Tính diện tích của hình phẳng được tô màu trong Hình 4.29.

Tính diện tích của hình phẳng giới hạn bởi các đường:

a) y = e^x, y = x² – 1, x = −1, x = 1;

b) y = sinx, y = x, \(x = \frac{\pi }{2},x = \pi \);

c) y = 9 – x², y = 2x², \(x = – \sqrt 3 ,x = \sqrt 3 \);

d) \(y = \sqrt x ,\)y = x², x = 0, x = 1.

Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi x là đại diện cho phần trăm số gia đình trong một quốc gia và y là phần trăm tổng thu nhập, mô hình y = x sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz y = f(x), biểu thị phân phối thu nhập thực tế. Diện tích giữa hai mô hình này, với 0 ≤ x ≤ 100, biểu thị “sự bất bình đẳng về thu nhập” của một quốc gia. Năm 2005, đường con Lorenz của Hoa Kỳ có thể được mô hình hóa bởi hàm số

y = (0,00061x² + 0,0218x + 1723)², 0 ≤ x ≤ 100,

trong đó x được tính từ các gia đình nghèo nhất đến giàu có nhất (Theo R.Larson, Brief Calculus: An Applied Approach, 8^th edition, Cengage Learning, 2009).

Tìm sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005.

Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: y = 2x – x², y = 0, x = 0, x = 2.

Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình $y=\sqrt{R^2-x^2}$, trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.

Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và $\widehat{AOB}=\alpha \left(0<\alpha \le \frac{\pi }{4}\right)$. Gọi β là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox (H.4.31).

a) Tính thể tích V của β theo a và α.

b) Tìm α sao cho thể tích V lớn nhất.