Câu hỏi
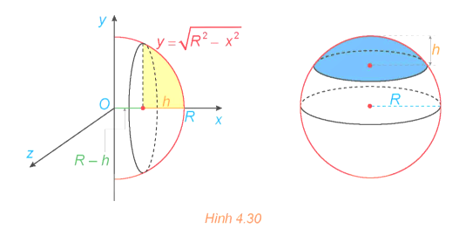
17/12/2024Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình , trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Thể tích cần tìm là:
\(V = \pi \int\limits_{R – h}^R {\left( {{R^2} – {x^2}} \right)dx} \)\( = \pi \left. {\left( {{R^2}x – \frac{{{x^3}}}{3}} \right)} \right|_{R – h}^R\)
\( = \pi \left( {{R^3} – \frac{{{R^3}}}{3} – {R^2}\left( {R – h} \right) + \frac{{{{\left( {R – h} \right)}^3}}}{3}} \right)\)\( = \pi \left( {{R^3} – \frac{{{R^3}}}{3} – {R^3} + {R^2}h + \frac{{{R^3}}}{3} – {R^2}h + R{h^2} – \frac{{{h^3}}}{3}} \right)\)
\( = \pi \left( {R{h^2} – \frac{{{h^3}}}{3}} \right)\)\( = \pi {h^2}\left( {R – \frac{h}{3}} \right)\).