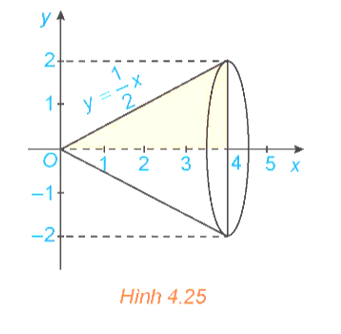
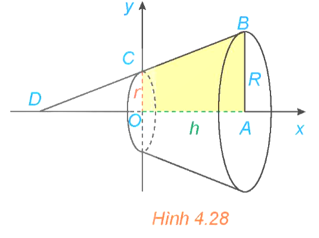
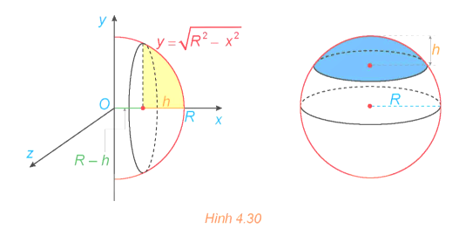
Câu hỏi
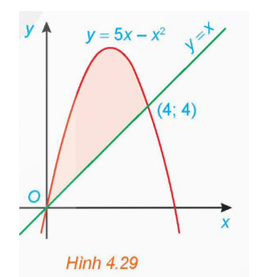
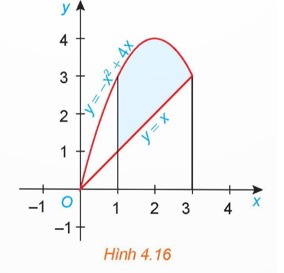
17/12/2024 2Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x2 + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16).
a) Giả sử S1 là diện tích hình phẳng giới hạn bởi parabol y = −x2 + 4x, trục hoành và hai đường thẳng x = 1, x = 3; S2 là diện tích hình phẳng giới hạn bởi đường thẳng y = x, trục hoành và hai đường thẳng x = 1, x = 3. Tính S1, S2 và từ đó suy ra S.
b) Tính và so sánh với S.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Ta có \({S_1} = \int\limits_1^3 {\left| { – {x^2} + 4x} \right|dx} \)\( = \int\limits_1^3 {\left( { – {x^2} + 4x} \right)dx} \)\( = \left. {\left( { – \frac{{{x^3}}}{3} + 2{x^2}} \right)} \right|_1^3\)\( = 9 – \frac{5}{3} = \frac{{22}}{3}\).
\({S_2} = \int\limits_1^3 {\left| x \right|} dx\)\( = \int\limits_1^3 x dx\)\( = \left. {\frac{{{x^2}}}{2}} \right|_1^3 = \frac{9}{2} – \frac{1}{2} = 4\).
Do đó S = S1 – S2 = \(\frac{{22}}{3} – 4 = \frac{{10}}{3}\).
b) Ta có \(\int\limits_1^3 {\left| {f\left( x \right) – g\left( x \right)} \right|} dx\)\( = \int\limits_1^3 {\left| { – {x^2} + 4x – x} \right|} dx\)\( = \int\limits_1^3 {\left| { – {x^2} + 3x} \right|} dx\)\( = \int\limits_1^3 {\left( { – {x^2} + 3x} \right)} dx\)
\( = \left. {\left( { – \frac{{{x^3}}}{3} + 3.\frac{{{x^2}}}{2}} \right)} \right|_1^3\)\( = \frac{9}{2} – \frac{7}{6} = \frac{{10}}{3}\).
Do đó \(S = \int\limits_1^3 {\left| {f\left( x \right) – g\left( x \right)} \right|} dx\).