Câu hỏi
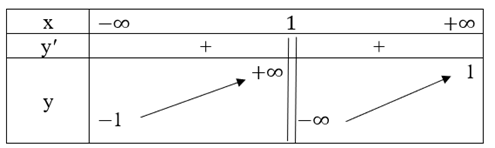
22/11/2024 1Cho hàm số \(y = f(x) = \frac{{\sqrt {{x^2} + 3} }}{{x – 1}}\) có đồ thị như hình sau:
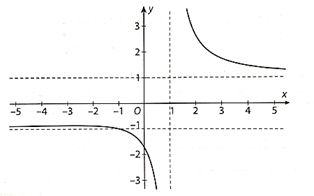
Hãy tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt {{x^2} + 3} }}{{x – 1}} = + \infty \);
\(\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{\sqrt {{x^2} + 3} }}{{x – 1}} = – \infty \).
Vì vậy, đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {{x^2} + 3} }}{{x – 1}} = – 1\);
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 3} }}{{x – 1}} = 1\).
Vì vậy, đường thẳng y = 1 và y = −1 là đường tiệm cận ngang của đồ thị hàm số.