Câu hỏi
22/11/2024 8Cho hàm số \(y = f(x) = \frac{{x + 2}}{{x – 3}}\) có đồ thị (C). Gọi tổng khoảng cách từ một điểm (x; y) ∈ (C), với x > 3, tới hai đường tiệm cận của (C) là g(x). Tìm các đường tiệm cận của đồ thị hàm số y = g(x).
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
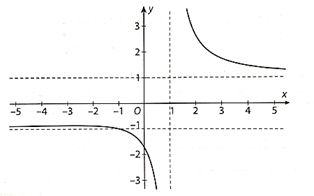
Đồ thị hàm số f(x) có đường tiệm cận đứng là đường thẳng x = 3 và đường tiệm cận ngang là đường thẳng y = 1.
Khoảng cách từ điểm M(x; y) ∈ (C), x > 3 đến tiệm cận đứng là d1 = x – 3.
Khoảng cách từ điểm M đến đường tiệm cận ngang là d2 = \(\frac{{x + 2}}{{x – 3}} – 1 = \frac{5}{{x – 3}}\).
Vậy g(x) = d1 + d2 = x – 3 + \(\frac{5}{{x – 3}}\).
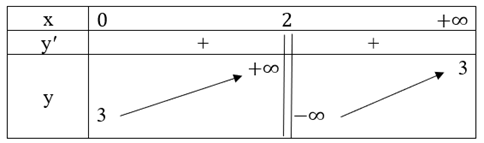
Ta có: \(\mathop {\lim }\limits_{x \to – \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to – \infty } \left[ {x–3 + \frac{5}{{x – 3}}\;} \right] = – \infty .\);
\(\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {x–3 + \frac{5}{{x – 3}}\;} \right] = + \infty .\)
Vì vậy đồ thị hàm số g(x) không có tiệm cận ngang
\(\mathop {\lim }\limits_{x \to {3^ – }} g\left( x \right) = \mathop {\lim }\limits_{x \to {3^ – }} \left[ {x–3 + \frac{5}{{x – 3}}\;} \right] = – \infty .\);
\(\mathop {\lim }\limits_{x \to {3^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {3^ + }} \left[ {x–3 + \frac{5}{{x – 3}}\;} \right] = + \infty .\)
Vì vậy, đường thẳng x = 3 là đường tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {g\left( x \right) – (x – 3)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x–3 + \frac{5}{{x – 3}} – (x – 3)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{5}{{x – 3}} = 0.\)
Vì vậy đường thẳng y = x – 3 là đường tiệm cận xiên của đồ thị hàm số.