Câu hỏi
22/11/2024 5Cho hàm số \(y = \frac{{x + 1}}{{x – 1}}\) có đồ thị (C).
Tính tích khoảng cách từ một điểm tùy ý thuộc (C) đến hai đường tiệm cận của nó.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Ta có: \(\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } \frac{{x + 1}}{{x – 1}} = 1\);
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x – 1}} = 1\).
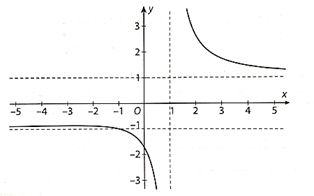
Vậy, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x – 1}} = + \infty \);
\(\mathop {\lim }\limits_{x \to {1^ – }} y = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{x + 1}}{{x – 1}} = – \infty \).
Vậyđường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Do đó đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng x = 1 và tiệm cận ngang
y = 1.
Lấy M(x0; y0) ∈ (C) với \({y_0} = \frac{{{x_0} + 1}}{{{x_0} – 1}}\).
Ta có: khoảng cách từ M đến đường tiệm cận đứng là d1 = | x0 – 1|, khoảng cách từ M đến tiệm cận ngang là d2 = \(\left| {\frac{{{x_0} + 1}}{{{x_0} – 1}} – 1} \right| = \frac{2}{{\left| {{x_0} – 1} \right|}}\).
Do đó tích khoảng cách là:d1d2 = \(\left| {{x_0}–1} \right|\). \(\frac{2}{{\left| {{x_0} – 1} \right|}}\) = 2.