Câu hỏi
04/12/2024 2Cắt bỏ hình quạt AOB (hình phẳng có nét gạch trong hình dưới đây) từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của hình quạt tròn còn lại với nhau để được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của quạt tròn dùng làm phễu (0 < x < 2π).
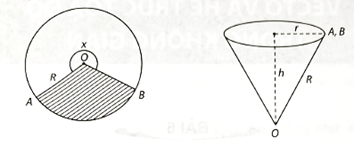
a) Hãy biểu diễn bán kính đáy r và đường cao h của hình nón theo P và x.
b) Tính thể tích của hình nón theo R và x.
c) Tìm x để hình nón có thể tích lớn nhất và tính giá trị lớn nhất đó.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Do độ dài của đường tròn đáy hình nón bằng độ dài của quạt tròn dùng làm phễu nên ta có: 2πr = Rx ⇔ r = \(\frac{{Rx}}{{2\pi }}\).
Mặt khác h = \(\sqrt {{R^2} – {r^2}} \) = \(\sqrt {{R^2} – \frac{{{R^2}{x^2}}}{{4{\pi ^2}}}} \) = \(\frac{R}{{2\pi }}\sqrt {4{\pi ^2} – {x^2}} \).
b) Thể tích của hình nón là:
V = \(\frac{1}{3}\pi {r^2}h\) = \(\frac{{{R^3}}}{{24{\pi ^2}}}{x^2}\sqrt {4{\pi ^2} – {x^2}} \), 0 < x < 2π.
c) Ta cần tìm x ∈ (0; 2π) sao cho thể tích V đạt giá trị lớn nhất.
Xét hàm số f(x) = \(\frac{{{R^3}}}{{24{\pi ^2}}}{x^2}\sqrt {4{\pi ^2} – {x^2}} \), x ∈ (0; 2π).
Ta có: f‘(x) = \(\frac{{{R^3}}}{{24{\pi ^2}}}.\frac{{x\left( {8{\pi ^2} – 3{x^2}} \right)}}{{\sqrt {4{\pi ^2} – {x^2}} }}\)
f‘(x) = 0 ⇔ x = \(\frac{{2\pi \sqrt 6 }}{3}\)≈ 1,63π.
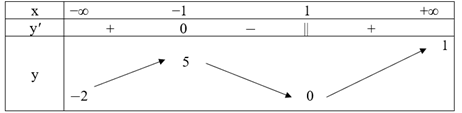
Ta có bảng biến thiên như sau:

Hình nón có thể tích lớn nhất khi x = \(\frac{{2\pi \sqrt 6 }}{3}\)≈ 1,63π.
Khi đó: \(\mathop {\max }\limits_{x \in (0;2\pi )} V = f\left( {\frac{{2\pi \sqrt 6 }}{3}} \right) = \frac{{2\sqrt 3 }}{{27}}\pi {R^3}\).