Câu hỏi
04/12/2024 5Cho hàm số y = x3 – 3x2 + 2 có đồ thị (C).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến ∆ của đồ thị (C) tại tâm đối xứng của nó. Chứng minh rằng ∆ là tiếp tuyến có hệ số góc nhỏ nhất của (C).
c) Tìm các giá trị của tham số m để phương trình x3 – 3x2 – m = 0 có ba nghiệm phân biệt.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
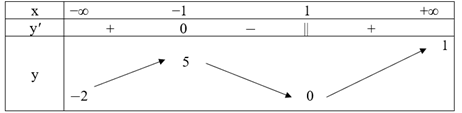
a) Tập xác định: D = ℝ.
Ta có: y‘ = 3x2 – 6x2
y‘ = 0 ⇔ 3x2 – 6x2 = 0 ⇔ x = 0 hoặc x = 2.
Hàm số đồng biến trên khoảng (−∞; 0) và (2; +∞).
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại điểm x = 0 và yCĐ = y(0) = 2.
Hàm số đạt cực tiểu tại điểm x = 2 và yCT = y(2) = −2.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to – \infty } y = – \infty \)
Ta có bảng biến thiên như sau:

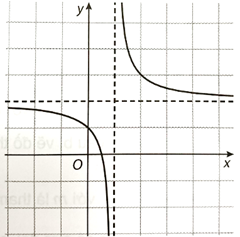
Đồ thị hàm số đi qua các điểm: (3; 2); (2; −2); (−1; −2); (0; 2).
Đồ thị hàm số có tâm đối xứng là điểm (1; 0).
Đồ thị hàm số như sau:

b) Tâm đối xứng của đồ thị hàm số là điểm I(1; 0).
Ta có: y‘(1) = −3.
Do đó phương trình tiếp tuyến của đồ thị hàm số tại tâm đối xứng của nó là:
y = y‘(1)(x – 1) + y(1)
= −3(x – 1) + 0
= −3x + 3 (∆).
Ta có: y‘ = 3x2 – 6x = 3(x2 – 2x + 1) – 3 = 3(x – 1)2 – 3 ≥ −3 với mọi x.
Do đó ∆ là tiếp tuyến có hệ số góc nhỏ nhất của (C).
c) Ta có: x3 – 3x2 – m = 0 ⇔ x3 – 3x2 + 2 = m + 2.
Vì vậy phương trình x3 – 3x2 – m = 0 là phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng y = m + 2. Suy ra, phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi đường thẳng y = m + 2 cắt đồ thị (C) tại 3 điểm phân biệt, điều này tương đương với −2 < m + 2 < 2 ⇔ −4 < m < 0.