Câu hỏi
04/12/2024 2Cho hàm số \(y = \frac{{m{x^2} + \left( {2m – 1} \right)x – 1}}{{x + 2}}\) với m là tham số.
a) Chứng minh rằng hàm số đã cho luôn có cực đại, cực tiểu với mọi m > 0.
b) Khảo sát và vẽ đồ thị (H) của hàm số đã cho với m = 1.
c) Giả sử ∆ cắt tiệm cận đứng và tiệm cận xiên của (H) tại điểm M ∈ (H) bất kì. Chứng minh rằng nếu ∆ cắt tiệm cận đứng và tiệm cận xiên của (H) tại A và B thì M luôn là trung điểm của đoạn AB.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Tập xác định: D = ℝ\{−2}.
Ta có: \(y’ = \frac{{m{x^2} + 4mx + 4m – 1}}{{{{\left( {x + 2} \right)}^2}}}\)
y‘ = 0 ⇔ mx2 + 4mx + 4m – 1 = 0
Xét ∆‘ = 4m2 – m(4m – 1) = 4m2 – 4m2 + m = m.
Với m > 0 thì ta được y‘ = 0 là phương trình bâc hai có hai nghiệm phân biệt x1, x2.
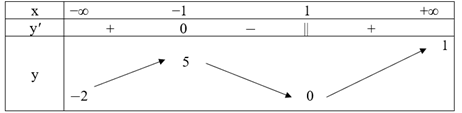
Bảng biến thiên của hàm số như sau:

Do đó hàm số luôn có cực đại, cực tiểu với mọi m > 0.
b) Với m = 1, ta có: y = \(\frac{{{x^2} + x – 1}}{{x + 2}}\)
Tập xác định: D = ℝ\{−2}.
Ta có: \(y’ = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\)
y‘ = 0 ⇔ x2 + 4x + 3 = 0 ⇔ x = −3 hoặc x = −1.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to – \infty } y = – \infty \) .
\(\mathop {\lim }\limits_{x \to – {2^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to – {2^ – }} y = – \infty \).
Vì vậy, đồ thị hàm số nhận đường thẳng x = −2 làm tiệm cận đứng.
Ta có: y = \(\frac{{{x^2} + x – 1}}{{x + 2}}\)= x – 1 + \(\frac{1}{{x + 2}}\).
Suy ra \(\mathop {\lim }\limits_{x \to + \infty } \left[ {y – \left( {x – 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 2}} = 0\)
Vì vậy, đường thẳng y = x – 1 là tiệm cận xiên của đồ thị hàm số.
Ta có bảng biến thiên như sau:

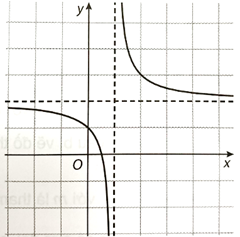
Đồ thị của hàm số như sau:
 ‘(t)(x – t) + y(t)
‘(t)(x – t) + y(t)
y = \(\frac{{{t^2} + 4t + 3}}{{{{\left( {t + 2} \right)}^2}}}\left( {x – t} \right) + \frac{{{t^2} + t – 1}}{{t + 2}}\).
Tiếp tuyến d cắt tiệm cận đứng tại điểm A\(\left( { – 2; – \frac{{3t + 4}}{{t + 2}}} \right)\).
Tiếp tuyến d cắt tiệm cận xiên tại điểm B(2t + 2; 2t + 1).
Ta có: \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2t = 2{x_M}\\{y_A} + {y_B} = (2t + 1) – \frac{{3t + 4}}{{t + 2}} = \frac{{2{t^2} + 2t – 2}}{{t + 2}} = 2{y_M}\end{array} \right.\).
Vì vậy M là trung điểm của đoạn AB.