Câu hỏi
04/12/2024 2Cho hàm số \(y = \frac{{{x^2} + mx + 1}}{{x + m}}\). Hàm số đạt cực đại tại x = 2 khi
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Đáp án đúng: A
Tập xác định: D = ℝ\{−m}.
Ta có: y‘ = \(\frac{{\left( {x + m + 1} \right)\left( {x + m – 1} \right)}}{{{{\left( {x + m} \right)}^2}}}\)
y‘ = 0 ⇔ \(\frac{{\left( {x + m + 1} \right)\left( {x + m – 1} \right)}}{{{{\left( {x + m} \right)}^2}}}\) = 0 ⇔ x = −m – 1 hoặc x = 1 – m.
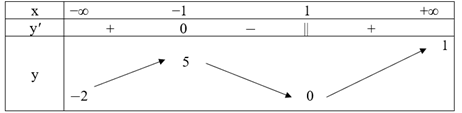
Nhận thấy, với mọi m luôn có −m – 1 < 1 – m.
Ta có bảng biến thiên như sau:

Để hàm số đạt cực đại tại x = 2 thì −m – 1 = 2 hay m = −1.
Vì vậy m = −1.