Câu hỏi
04/12/2024 8Cho hàm số y = \(\frac{1}{3}\)x3 + (m – 1)x2 + (2m – 3)x + \(\frac{2}{3}\).
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.
b) Tìm m để hàm số có hai điểm cực trị x1 và x2 thỏa mãn \(x_1^2 + x_2^2 = 5\).
c) Tìm m để hàm số đồng biến trên ℝ.
d) Tìm m để hàm số đồng biến trên khoảng (1; +∞).
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Khi m = 2, ta có: y = \(\frac{1}{3}\)x3 + x2 + x + \(\frac{2}{3}\).
y‘ = x2 + 2x + 1 = (x + 1)2 ≥ 0 với mọi x.
Hàm số luôn đồng biến trên ℝ.
Hàm số không có cực trị.
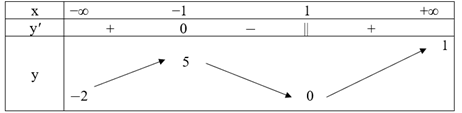
Bảng biến thiên của hàm số như sau:

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to – \infty } y = – \infty \)
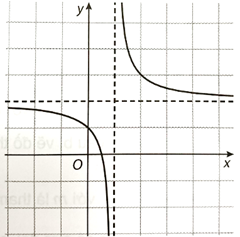
Đồ thị hàm số nhận điểm I\(\left( { – 1;\frac{1}{3}} \right)\) làm tâm đối xứng. Đồ thị hàm số có hình vẽ như sau:

b) Ta có: y = \(\frac{1}{3}\)x3 + (m – 1)x2 + (2m – 3)x + \(\frac{2}{3}\)
y‘ = x2 + 2(m – 1)x + 2m – 3
y‘ = x2 + 2mx – 2x + 2m – 3
y‘ = (x2 – 2x – 3) + (2mx + 2m)
y‘ = (x + 1)(x – 3) + 2m(x + 1).
y‘ = (x + 1) (x – 3 + 2m)
y‘ = 0 khi x = −1 hay x = 3 – 2m
Để hàm số có hai nghiệm phân biệt thì x1 ≠ x2 hay 3 – 2m ≠ −1 hay m ≠ 2.
Ta có: \(x_1^2 + x_2^2 = 5\)
(−1)2 + (3 – 2m)2 = 5
(3 – 2m)2 = 4
Suy ra 3 – 2m = 2 hoặc 3 – 2m = −2
⇒ m = \(\frac{5}{2}\) hoặc m \(\frac{1}{2}\).
Vì vậy m ∈ \(\left\{ {\frac{5}{2};\frac{1}{2}} \right\}\).
c) Ta có: y‘ = x2 + 2(m – 1)x + 2m – 3
Để hàm số đồng biến trên ℝ ⇔ \(\left\{ \begin{array}{l}a = 1 > 0\\\Delta \le 0\end{array} \right.\)⇔ \(\left\{ \begin{array}{l}a = 1 > 0\\4{\left( {m – 1} \right)^2} – 4\left( {2m – 3} \right) \le 0\end{array} \right.\)
m2 – 2m + 1 – 2m + 3 ≤ 0
m2 – 4m + 4 ≤ 0
(m – 2)2 ≤ 0
⇒ m = 2.
d) Ta có: y‘ = x2 + 2(m – 1)x + 2m – 3
y‘ = 0 ⇔ \(\left[ \begin{array}{l}x = – 1\\x = 3 – 2m\end{array} \right.\)
Trường hợp 1: −1 ≤ 3 – 2m ⇔ m ≤ 2. Ta có bảng biến thiên như sau:

Để hàm số đồng biến trên (1; +∞) thì 3 – 2m ≤ 1 ⇔ m ≥ 1.
Vậy kết hợp điều kiện ta được 1 ≤ m ≤ 2.
Trường hợp 2: 3 – 2m < −1 ⇔ m > 2. Có bảng biến thiên như sau:

Trường hợp này hàm số đồng biến trên (−1; +∞) nên hiển nhiên đồng biến trên (1; +∞).
Do đó trường hợp này m > 2.
Vậy hàm số đồng biến trên khoảng (1; +∞) khi và chỉ khi m ≥ 1.