Câu hỏi
04/12/2024 2Một hành lang giữa hai nhà có hình dạng một lăng trụ đứng (xem hình bên). Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC.
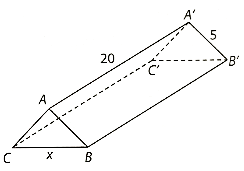
a) Tính thể tích V của hình lăng trụ theo x.
b) Tìm x sao cho hình lăng trụ có thể tích lớn nhất và tính giá trị lớn nhất đó.
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Ta có:

Kẻ AH là chiều cao của tam giác ABC
Lúc này, AH = \(\sqrt {A{C^2} – H{C^2}} \) = \(\sqrt {25 – {{\left( {\frac{x}{2}} \right)}^2}} \) = \(\frac{1}{2}\sqrt {100 – {x^2}} \).
Diện tích tam giác ABC là:
S∆ABC = \(\frac{1}{2}\)BC. AH = \(\frac{1}{2}\)x\(\frac{1}{2}\sqrt {100 – {x^2}} \) = \(\frac{1}{4}x\sqrt {100 – {x^2}} \).
Thể tích khối lăng trụ là:
V = S∆ABC. AA‘ = 5x\(\sqrt {100 – {x^2}} \) (m3) với 0 < x < 10.
b) Xét hàm số thể tích f(x) = 5x\(\sqrt {100 – {x^2}} \) trên khoảng (0; 10).
Ta có: f‘(x) = 5\(\sqrt {100 – {x^2}} \) + 5x.\(\frac{{ – 2x}}{{2\sqrt {100 – {x^2}} }}\) = \(\frac{{500 – 10{x^2}}}{{\sqrt {100 – {x^2}} }}\);
f‘(x) = 0 ⇔ x = \(5\sqrt 2 \) (x > 0).
Ta có bảng biến thiên:

Vậy hình lăng trụ có thể tích lớn nhất khi x = \(5\sqrt 2 \) (m).
Vì vậy \(\mathop {\max }\limits_{x \in (0;10)} V = V\left( {5\sqrt 2 } \right) = 250\)(m3).