Câu hỏi
04/12/2024 1Cho hàm số y = \(\frac{1}{{\sqrt x }}\). Xét các mệnh đề sau:
(I) Hàm số nghịch biến trên tập xác định của nó.
(II) Trục hoành là tiệm cận ngang của đồ thị hàm số.
(III) Trục tung là tiệm cận đúng của đồ thị hàm số.
(IV) Hàm số không có cực trị.
Số mệnh đề đúng trong các mệnh đề trên là:
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
Đáp án đúng: D
Tập xác định: D = (0; +∞).
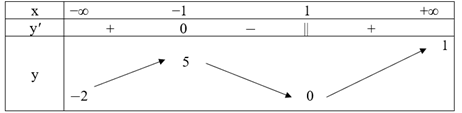
Ta có: y‘ = \(\frac{{ – 1}}{{2\sqrt {{x^3}} }}\) < 0 với mọi x ∈ D.
Hàm số nghịch biến trên tập xác định của nó.
Hàm số không có cực trị.
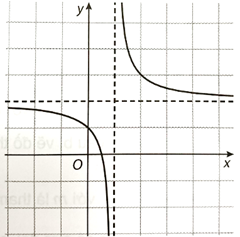
Giới hạn tại vô cực, giới hạn vô cực: \(\mathop {\lim }\limits_{x \to + \infty } y = 0;\mathop {\lim }\limits_{x \to – \infty } y = 0\)
Vậy, đường thẳng y = 0 (trục tung) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to {0^ – }} y = – \infty \)
Do đó, đường thẳng x = 0 (trục hoành) là tiệm cận đứng của đồ thị hàm số.
Vì vậy có tất cả 4 mệnh đề đúng.