Câu hỏi
04/12/2024 2Cho hàm số \(y = \frac{{\left( {m + 1} \right)x – 2m + 1}}{{x – 1}}\).
a) Tìm m để tiệm cận ngang của đồ thị hàm số đi qua điểm (1; 2).
b) Khảo sát và vẽ đồ thị (H) của hàm số y = f(x) với m tìm được ở câu a.
c) Từ đồ thị (H) của hàm số y = f(x) ở câu b, vẽ đồ thị của hàm số y = \(\left| {f(x)} \right|\).
Câu hỏi thuộc đề thi
Danh mục liên quan
Lời giải của Vua Trắc Nghiệm
a) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {m + 1} \right)x – 2m + 1}}{{x – 1}} = m + 1\);
\(\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } y\frac{{\left( {m + 1} \right)x – 2m + 1}}{{x – 1}} = m + 1\).
Vậy tiệm cận ngang là đường thẳng y = m + 1.
Để tiệm cận ngang của đồ thị hàm số đi qua điểm (1; 2) thì m + 1 = 2 hay m = 1.
Vậy m = 1.
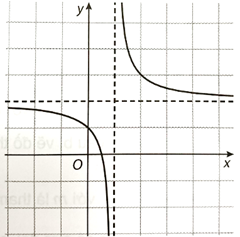
b) Với m = 1, hàm số trở thành \(y = \frac{{2x – 1}}{{x – 1}}\).
Tập xác định: D = ℝ\{1}.
Ta có: \(\frac{{ – 1}}{{{{\left( {x – 1} \right)}^2}}}\) < 0, với mọi x ≠ 1.
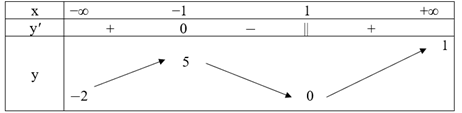
Suy ra hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x – 1}}{{x – 1}} = 2\),
\(\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } \frac{{2x – 1}}{{x – 1}} = 2\).
Vì vậy, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{2x – 1}}{{x – 1}} = + \infty \),
\(\mathop {\lim }\limits_{x \to {1^ – }} y = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{2x – 1}}{{x – 1}} = – \infty \).
Vì vậy, đồ thị nhận đường thẳng x = 1 làm tiệm cận đứng.
Bảng biến thiên của hàm số được cho như sau:

Đồ thị hàm số như sau:

c) Ta có:
\(y = \left| {f(x)} \right| = \left\{ \begin{array}{l}f(x){\rm{ khi f(x) }} \ge {\rm{ 0}}\\ – f(x){\rm{ khi f(x) < 0}}{\rm{.}}\end{array} \right.\)
Vì vậy, để vẽ đồ thị hàm số y = \(\left| {f(x)} \right|\) ta làm như sau: Giữ nguyên phần đồ thị hàm số
y = f(x) ở phía trên trục Ox; lấy đối xứng qua trục Ox phần đồ thị hàm số y = f(x) ở phía trên trục Ox. Đồ thị y = \(\left| {f(x)} \right|\) là đường liền nét trong hình vẽ dưới đây: